Cách Tính Hệ Số Tương Quan

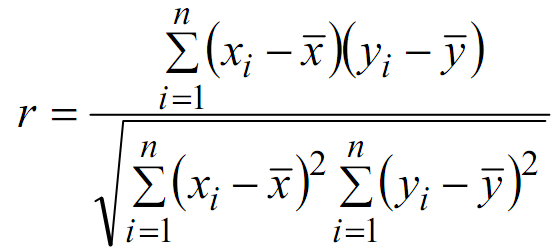
Có bao giờ bạn thắc mắc tại sao một số yếu tố lại có mối liên hệ chặt chẽ với nhau? Hệ số tương quan chính là công cụ giúp chúng ta lý giải điều đó. Trong cuộc sống, từ mối quan hệ giữa thời tiết và doanh thu bán hàng đến sự tương tác giữa học tập và điểm số, hệ số tương quan mang đến cái nhìn sâu sắc về cách các biến số ảnh hưởng lẫn nhau. Trong bài viết này, chúng ta sẽ cùng khám phá cách tính hệ số tương quan, giúp bạn đọc hiểu rõ hơn về mối liên hệ thú vị giữa các yếu tố trong thế giới xung quanh.

Cách Tính Hệ Số Tương Quan

Hệ số tương quan (correlation coefficient) là một chỉ số cực kỳ hữu ích trong thống kê, giúp chúng ta đo lường mức độ và chiều hướng của mối quan hệ giữa hai biến số. Giá trị của hệ số này nằm trong khoảng từ -1 đến 1. Khi hệ số r = 1, điều đó có nghĩa là có một mối quan hệ tuyến tính hoàn hảo giữa hai biến. Ngược lại, nếu r = -1, nghĩa là mối quan hệ ngược chiều hoàn hảo.

Khi tính hệ số tương quan bằng R, có một số phương pháp phổ biến, nhưng phương pháp Pearson được sử dụng nhiều nhất. Hệ số này cho biết độ mạnh yếu của mối quan hệ; nếu r càng tiến gần đến 1 hoặc -1, thì mối quan hệ càng chặt chẽ. Nếu r gần 0, điều đó cho thấy không có mối tương quan đáng kể nào.

Ngoài ra, chúng ta cũng có thể sử dụng hệ số tương quan Kendall τ để nắm bắt các cặp số “song hành” trong dữ liệu. Việc lựa chọn phương pháp phụ thuộc vào đặc điểm của dữ liệu và mục tiêu phân tích của bạn. Việc áp dụng hàm CORREL trong Excel cũng giúp chúng ta tính nhanh chóng hệ số tương quan giữa hai tập dữ liệu.

Công Thức Tính Hệ Số Tương Quan Pearson

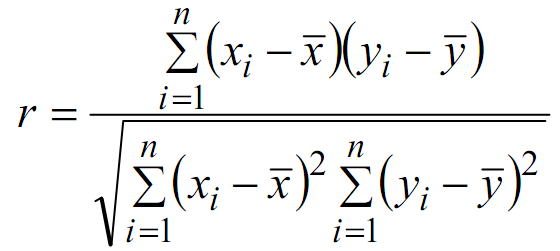
Hệ số tương quan Pearson là một công cụ mạnh mẽ trong phân tích định lượng, giúp chúng ta hiểu rõ hơn về mối liên hệ giữa hai biến số. Hệ số này, được ký hiệu là r, có phạm vi từ -1 đến 1. Nếu r = 1, điều này cho thấy hai biến có mối quan hệ tuyến tính hoàn hảo. Ngược lại, nếu r = 0, hai biến gần như không có liên hệ nào với nhau.

Để tính hệ số tương quan Pearson, chúng ta sử dụng công thức: Corr(X, Y) = Cov(X, Y) / (Var(X) * Var(Y)). Trong đó, Cov là hiệp phương sai và Var là phương sai của các biến tương ứng. Khi áp dụng phân tích này trong SPSS, bạn không cần phải tính toán thủ công, chỉ cần sử dụng hàm PEARSON để có được hệ số tương quan nhanh chóng và chính xác.

Phân tích sử dụng hệ số tương quan Pearson thường được thực hiện qua sáu bước cơ bản, từ việc thu thập dữ liệu, kiểm tra điều kiện của dữ liệu cho đến việc diễn giải kết quả. Việc nắm vững các bước này sẽ giúp bạn đưa ra những kết luận chính xác về mối quan hệ giữa các biến trong nghiên cứu của mình.

Hệ Số Tương Quan Trong Xác Suất Thống Kê

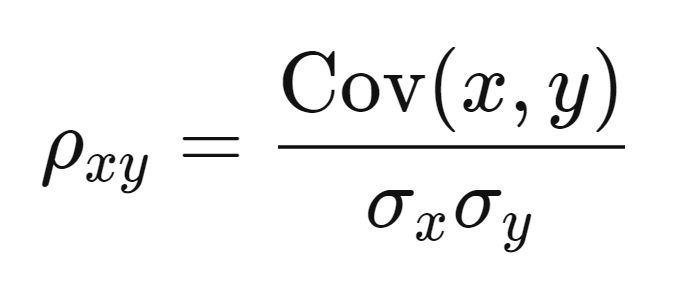
Hệ số tương quan là một công cụ hữu ích trong xác suất thống kê, giúp chúng ta đo lường mức độ mạnh yếu của mối quan hệ giữa hai biến số. Hệ số này được thể hiện qua các giá trị trong khoảng từ -1 đến 1. Ví dụ, nếu giá trị r bằng 1, đó là dấu hiệu cho thấy mối quan hệ tuyến tính hoàn hảo giữa hai biến. Ngược lại, giá trị r bằng -1 thể hiện mối quan hệ âm hoàn hảo.

Những trường hợp thực tế, khi hệ số r lớn hơn 0.7 hoặc nhỏ hơn -0.7 cho thấy mối liên hệ mạnh mẽ giữa các biến. Hệ số tương quan Pearson thường được áp dụng để đo lường tính liên kết này, trong khi hệ số tương quan Spearman được sử dụng cho dữ liệu không điều kiện.

Khi kiểm định thống kê, nếu giá trị sig nhỏ hơn 0.05, chúng ta có thể kết luận rằng cặp biến có tương quan tuyến tính. Điều này đặc biệt quan trọng trong đầu tư, giúp các nhà đầu tư đánh giá sự liên kết giữa các tài sản và yếu tố thị trường, từ đó đưa ra quyết định thông minh hơn.

Cách Tính Hệ Số Tương Quan Giữa X Và Y

Để tính toán hệ số tương quan giữa hai biến X và Y, trước tiên, ta cần tìm khoảng tin cậy 95% cho giá trị trung bình của X (µX) và Y (µY). Điều này giúp chúng ta xác định độ chính xác của các ước lượng này dựa trên mẫu dữ liệu. Tiếp theo, ta sẽ tính giá trị hệ số tương quan mẫu giữa X và Y. Hệ số này cho chúng ta thấy mức độ tương quan giữa hai biến. Nếu hệ số tương quan lớn hơn 1 hoặc nhỏ hơn -1, điều này cho thấy có lỗi trong quá trình tính toán.

Ngoài ra, khi hai biến không tuân theo luật phân phối chuẩn, ta có thể sử dụng hệ số tương quan Spearman thay vì Pearson. Trong trường hợp tiêu chuẩn hơn, hệ số tương quan Pearson là lựa chọn phổ biến nhất, được tính bằng cách chia hiệp phương sai cho tích của độ lệch chuẩn của hai biến. Qua đó, nếu giá trị hệ số tương quan gần 1 hoặc -1, điều này cho thấy một mối quan hệ tuyến tính chặt chẽ giữa X và Y. Việc ứng dụng các công cụ như Excel có thể giúp đơn giản hóa quá trình này thông qua hàm CORREL().

Cách Tính Hệ Số Tương Quan Mẫu

Hệ số tương quan mẫu, đặc biệt là hệ số Pearson’s r, là một công cụ mạnh mẽ để đánh giá mối quan hệ giữa hai biến. Để tính hệ số này, bạn có thể sử dụng máy tính bỏ túi hoặc phần mềm thống kê. Đơn giản chỉ cần nhập dữ liệu của hai biến và máy tính sẽ tự động tính toán.

Giá trị của hệ số tương quan r nằm trong khoảng từ -1 đến 1. Nếu r = 1, điều này có nghĩa là hai biến có mối quan hệ tuyến tính hoàn hảo. Ngược lại, nếu r = -1, mối quan hệ giữa chúng hoàn toàn ngược chiều. Khi giá trị của r tiến gần đến 0, tức là mối quan hệ tuyến tính giữa hai biến càng yếu. Hệ số tương quan mẫu không chỉ giúp bạn xác định được mối liên hệ mà còn cho biết mức độ chặt chẽ của nó.

Việc tìm phương trình đường hồi quy tuyến tính cũng dựa vào hệ số tương quan. Nó cho phép bạn dự đoán giá trị của một biến dựa trên giá trị của biến còn lại. Bằng cách này, bạn có thể hiểu rõ hơn về mối quan hệ giữa hai biến trong thực tế.

Cách Tính Hệ Số Tương Quan Trong Excel

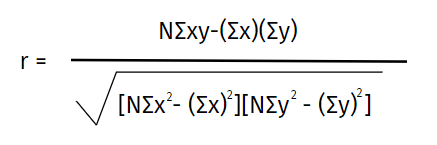
Hàm CORREL trong Excel là một công cụ hữu ích giúp bạn tính toán hệ số tương quan giữa hai tập dữ liệu. Hệ số tương quan này cho biết mức độ liên quan giữa hai biến, với giá trị nằm trong khoảng từ -1 đến 1. Nếu kết quả gần bằng +1, điều này cho thấy có một mối quan hệ dương hoàn hảo; ngược lại, giá trị gần -1 cho thấy mối quan hệ âm hoàn hảo. Hệ số bằng 0 có nghĩa là không có sự liên quan rõ rệt.

Để sử dụng hàm CORREL, trước tiên bạn cần mở tập dữ liệu trong bảng tính Excel. Chỉ cần nhập công thức =CORREL(mảng1, mảng2) vào ô bạn muốn hiển thị kết quả, trong đó mảng1 và mảng2 là các ô chứa dữ liệu của hai biến bạn muốn so sánh.

Bên cạnh việc dùng hàm CORREL, Excel còn cung cấp tính năng phân tích số liệu, giúp bạn hiểu rõ hơn về mối quan hệ giữa các biến. Chỉ với những bước đơn giản, bạn đã có thể khai thác sức mạnh của thống kê để đưa ra quyết định chính xác hơn.

Cách Tính Hệ Số Tương Quan Bằng Máy Tính

Để tính hệ số tương quan bằng máy tính Casio fx-570ES Plus, trước hết bạn cần vào menu thống kê. Tại đây, bạn sẽ nhập dữ liệu cho cả hai biến x và y. Việc nhập dữ liệu là rất quan trọng vì nó ảnh hưởng trực tiếp đến kết quả. Sau khi đã nhập đầy đủ, bạn cần tính tổng tích của dữ liệu x và y, cùng với độ lệch chuẩn mẫu của x và giá trị tối đa của y.

Khi đã hoàn tất việc nhập liệu, bạn chọn chế độ hồi quy tuyến tính. Trên màn hình, bạn sẽ thấy các giá trị như A, B, và đặc biệt là hệ số tương quan r. Để tìm ra giá trị của r, bạn chỉ cần chọn số tương ứng (thường là 3) và nhấn dấu bằng (=) để nhận kết quả.

Nếu bạn sử dụng máy tính Casio fx-580, quy trình tương tự vẫn được áp dụng, nhưng có thể có một vài chỉnh sửa nhỏ. Đừng quên rằng hệ số tương quan r sẽ giúp bạn đánh giá mức độ liên hệ giữa hai biến, vì vậy hãy dành thời gian để nhập dữ liệu chính xác.

Cuối cùng, việc tính hệ số tương quan không chỉ là một công cụ thống kê mà còn là một chiếc cầu nối giúp chúng ta hiểu rõ hơn về mối quan hệ giữa hai biến. Bằng cách áp dụng những bước đơn giản đã nêu, bạn có thể tự mình khám phá những kết nối thú vị trong dữ liệu của mình. Hãy nhớ rằng, dữ liệu chỉ thực sự có giá trị khi chúng ta biết cách lý giải và áp dụng chúng vào cuộc sống thực. Hy vọng rằng bài viết này đã mang đến cho bạn những thông tin bổ ích và giúp bạn tự tin hơn trong việc phân tích dữ liệu!