Trung Bình Và Trung Vị

Khi chúng ta nói đến thống kê, có hai khái niệm thường được nhắc đến là trung bình và trung vị. Nhưng bạn có bao giờ tự hỏi chúng thực sự có ý nghĩa như thế nào và tại sao chúng lại quan trọng trong đời sống hàng ngày? Trung bình giúp chúng ta có cái nhìn tổng quát về dữ liệu, còn trung vị lại cung cấp sự phản ánh chính xác hơn về điểm giữa của một tập hợp số liệu. Nếu bạn tò mò muốn tìm hiểu sâu hơn về cách hai khái niệm này ảnh hưởng đến những quyết định của chúng ta, hãy cùng khám phá nhé!

Trung Bình Và Trung Vị

Khi phân tích dữ liệu, hai khái niệm trung bình và trung vị thường xuất hiện và có vai trò quan trọng. Trung bình (mean) được tính bằng cách cộng tất cả các giá trị trong một tập hợp lại với nhau và chia cho số lượng giá trị. Đây là thước đo phổ biến nhất để xác định vị trí trung tâm của dữ liệu. Tuy nhiên, trung bình có thể bị ảnh hưởng lớn bởi các giá trị ngoại lệ.

Ngược lại, trung vị (median) lại là một khái niệm khác. Để tìm trung vị, người ta sẽ sắp xếp các giá trị theo thứ tự tăng dần và tìm giá trị ở giữa. Nếu số phần tử lẻ, trung vị là giá trị đứng giữa, còn nếu có số lượng chẵn, trung bình của hai giá trị giữa sẽ là trung vị. Trung vị thường được sử dụng khi dữ liệu lệch hoặc có nhiều giá trị ngoại lệ, nhằm phản ánh tốt hơn đặc điểm chung của tập dữ liệu.

Tóm lại, việc lựa chọn sử dụng trung bình hay trung vị phụ thuộc vào tính chất của dữ liệu. Nếu dữ liệu phân bố đồng đều thì trung bình là sự chọn lựa hợp lý. Nhưng nếu có nhiều ngoại lệ, trung vị sẽ giúp chúng ta có cái nhìn rõ ràng hơn về sự phân bố của các giá trị.

Trung Bình Và Trung Vị Tiếng Anh

Trung vị, trong tiếng Anh gọi là “median” (phát âm: /ˈmɛdiən/), là một khái niệm quan trọng trong thống kê. Nó đại diện cho số nằm ở giữa một tập dữ liệu đã được sắp xếp. Để tìm được trung vị, bạn chỉ cần sắp xếp các số theo thứ tự tăng dần và lấy số ở vị trí giữa. Nếu số lượng phần tử là lẻ, trung vị là số đơn lẻ ở giữa. Nếu số lượng là chẵn, bạn phải tính trung bình của hai giá trị ở giữa.

Một điểm thú vị là trung vị không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ, điều này làm cho nó trở thành một chỉ số đáng tin cậy hơn so với trung bình. Chẳng hạn, trong dãy số 2, 4, 6, 8 và 10, trung vị là 6. Tuy nhiên, nếu có một giá trị rất lớn như 100 trong dãy số này, giá trị trung bình sẽ bị kéo lên cao, trong khi trung vị vẫn giữ nguyên.

Những từ liên quan đến trung vị bao gồm “average” (trung bình), “skewed left” (lệch trái) và “skewed right” (lệch phải). Sự khác biệt giữa trung bình và trung vị rất quan trọng trong việc phân tích dữ liệu và hiểu rõ về xu hướng của một tập hợp số liệu.

Tính Trung Bình Và Trung Vị

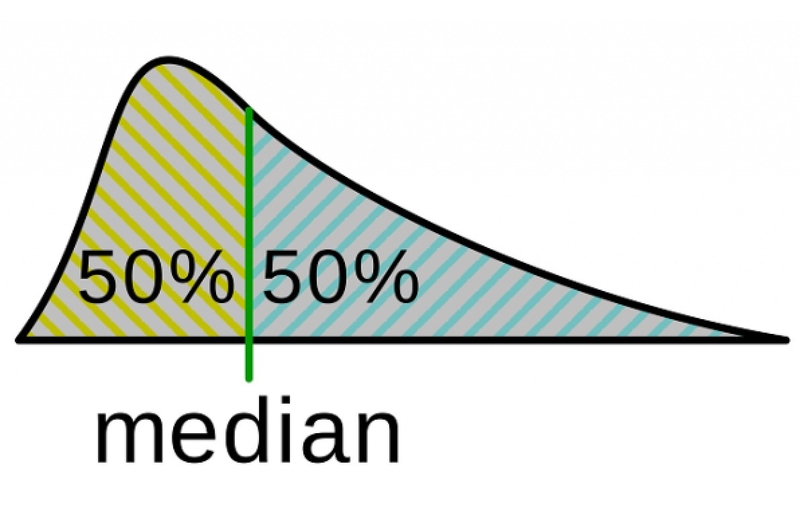
Tính trung bình và trung vị là hai khái niệm quan trọng trong thống kê, giúp chúng ta hiểu rõ hơn về dữ liệu mà chúng ta đang phân tích. Trung bình, hay số trung bình cộng, được tính bằng cách cộng tất cả các giá trị lại với nhau rồi chia cho số lượng giá trị. Phương pháp này thường được sử dụng để có được một giá trị đại diện cho toàn bộ tập hợp dữ liệu.

Trong khi đó, trung vị lại là một khái niệm khác. Trung vị được xác định là giá trị ở giữa dãy số khi chúng ta đã sắp xếp chúng theo thứ tự tăng dần. Nếu số lượng dữ liệu là lẻ, trung vị sẽ là số đứng ở giữa, còn nếu số lượng là chẵn, trung vị sẽ là trung bình của hai số giữa.

Cả hai cách tính này đều mang lại thông tin hữu ích, nhưng trong một số trường hợp, trung bình có thể bị ảnh hưởng bởi những giá trị ngoại lai, trong khi trung vị lại thể hiện tốt hơn về xu hướng phân phối của dữ liệu. Do đó, tuỳ thuộc vào mục đích phân tích mà chúng ta sẽ chọn sử dụng trung bình hay trung vị cho phù hợp.

Công Thức Tính Trung Vị

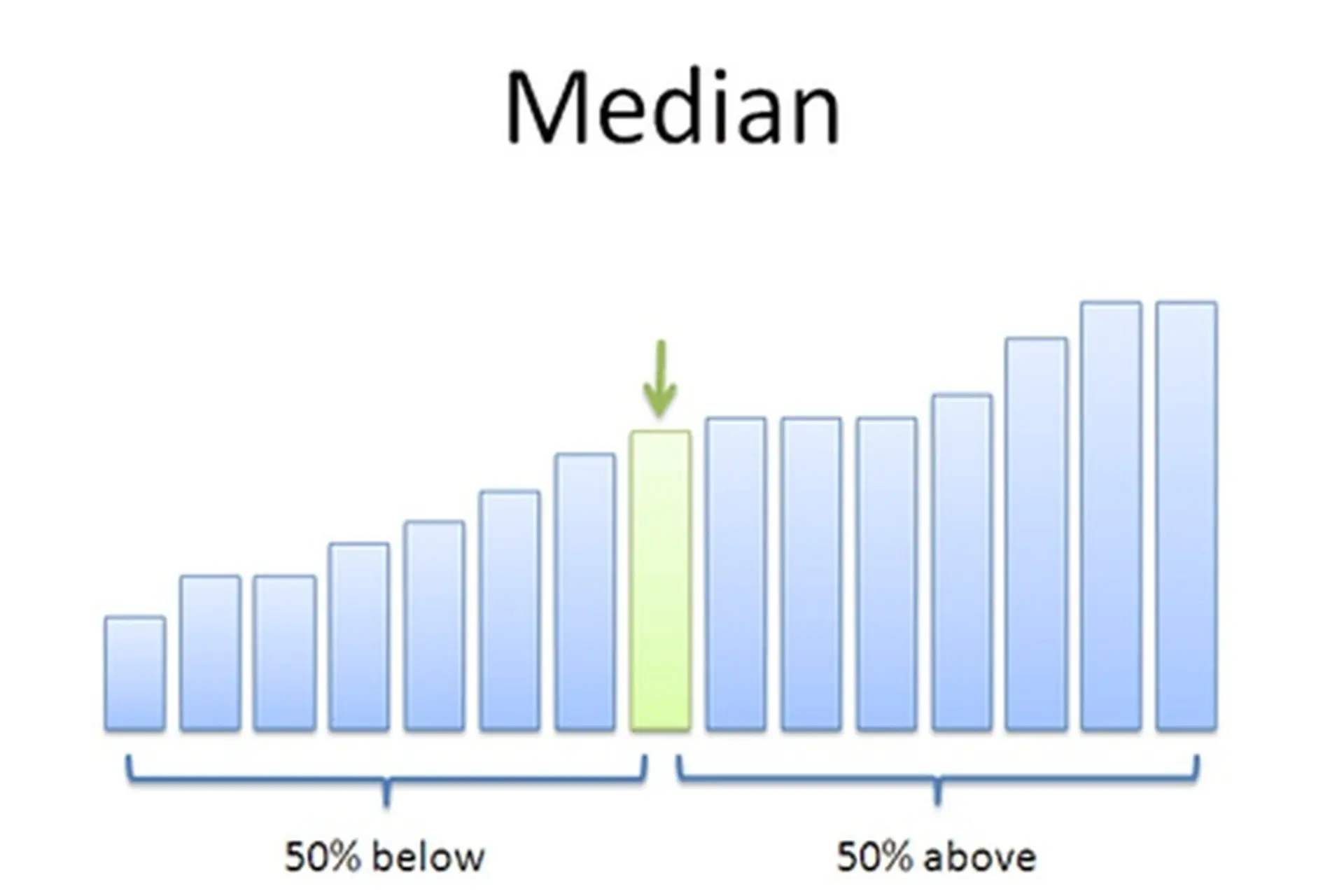
Trong thống kê, trung vị là một chỉ số quan trọng giúp chúng ta nắm bắt được giá trị trung bình của một tập hợp số liệu. Để tính trung vị, chúng ta cần sắp xếp các giá trị trong mẫu số liệu theo thứ tự tăng dần hoặc giảm dần. Nếu số lượng phần tử là lẻ, trung vị sẽ là giá trị đứng ở vị trí giữa. Ngược lại, nếu số lượng phần tử là số chẵn, trung vị được tính bằng cách lấy trung bình cộng của hai giá trị ở giữa.

Ngoài việc tính trung vị, tứ phân vị cũng là một công cụ hữu ích, bao gồm tứ phân vị thứ nhất (Q1), thứ hai (Q2), và thứ ba (Q3). Chúng giúp chia tập hợp số liệu thành các phần đều nhau, từ đó cho thấy sự phân bố của dữ liệu. Đối với mẫu số liệu ghép nhóm, trung vị có thể được tính theo công thức:

\[ M_e = u_m + \frac{n/2 – C}{n_m} \cdot (u_{m+1} – u_m) \].

Việc nắm vững cách tính trung vị và tứ phân vị không chỉ giúp các em học sinh lớp 11 giải quyết các bài toán thống kê mà còn trang bị kiến thức nền tảng cho những lĩnh vực học khác trong tương lai.

Tính Trung Vị Trong Thống Kê

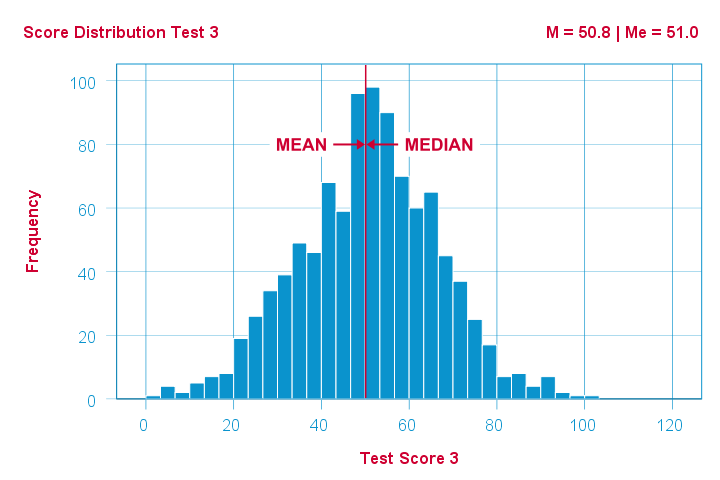
Tính trung vị trong thống kê là một phương pháp quan trọng để xác định giá trị trung tâm của một tập hợp số liệu. Trung vị, ký hiệu là Me, là giá trị đứng ở vị trí giữa khi các số liệu được sắp xếp theo thứ tự không giảm. Nếu số lượng số liệu là lẻ, dễ dàng xác định trung vị bằng cách chọn giá trị ở giữa. Ngược lại, nếu số lượng số liệu là chẵn, trung vị sẽ được tính bằng trung bình của hai giá trị nằm ở giữa dãy số.

Trung vị được sử dụng rộng rãi trong thống kê mô tả, đặc biệt trong các nghiên cứu xã hội, vì nó không bị ảnh hưởng bởi những giá trị ngoại lệ cao hoặc thấp. Điều này làm cho trung vị trở thành một chỉ số hữu ích khi dữ liệu có sự phân bố không đồng đều. Hơn nữa, trung vị cho chúng ta cái nhìn rõ ràng hơn về xu hướng trung tâm của một tập hợp mà không bị lệch do những giá trị cực trị.

Tóm lại, việc tính toán trung vị đơn giản nhưng mang lại giá trị thực tiễn cao, giúp người dùng nắm được bức tranh tổng thể về dữ liệu.

Trung Vị Là Q2

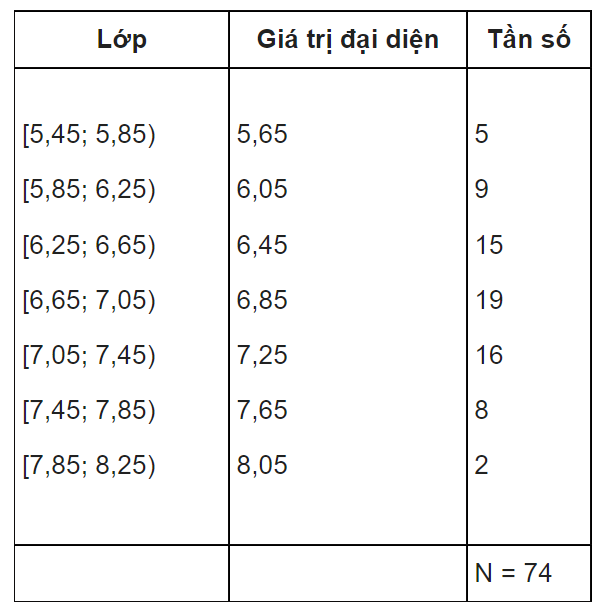
Trung vị, hay còn gọi là tứ phân vị thứ hai (Q2), chính là giá trị nằm ở giữa dãy số liệu khi chúng ta sắp xếp theo thứ tự tăng dần. Để hiểu rõ hơn, chúng ta có thể lấy ví dụ với tập dữ liệu 1, 2, 3, 4, 5. Ở đây, số 3 chính là trung vị, bởi nó nằm ở vị trí giữa và chia dãy số thành hai nửa bằng nhau.

Trong thống kê, Q2 thể hiện cho 50% dữ liệu, giúp chúng ta nhanh chóng nhận diện điểm phân chia trong một tập hợp. Ngoài Q2, còn có Q1 và Q3, phân chia dữ liệu thành các phần như 25% và 75%. Sự hiểu biết về các tứ phân vị này không chỉ giúp trong việc phân tích dữ liệu mà còn hỗ trợ trong các quyết định thực tiễn.

Khi xét đến mẫu số liệu ghép nhóm, trung vị vẫn giữ nguyên vai trò quan trọng. Việc xác định Q2 trong trường hợp này có thể thực hiện qua công thức nhất định, nhưng nguyên tắc cốt lõi vẫn là tìm ra điểm giữa của dãy số liệu đã được tổ chức. Như vậy, trung vị luôn là công cụ hữu ích trong thống kê, giúp trực quan hóa và hiểu rõ hơn về tập dữ liệu của chúng ta.

Cách Tính Sai Khác Giữa Số Trung Bình Và Số Trung Vị

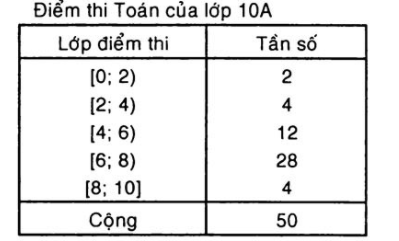
Khi so sánh số trung bình và số trung vị, chúng ta sẽ thấy hai khái niệm này rất khác nhau trong cách tính toán và ý nghĩa. Số trung bình được tính bằng cách cộng tất cả các giá trị lại với nhau và chia cho số lượng giá trị. Điều này có thể làm cho số trung bình bị ảnh hưởng mạnh mẽ bởi các giá trị cực trị, hay còn gọi là điểm outlier.

Ngược lại, số trung vị là giá trị nằm ở giữa của một dãy số sau khi đã được sắp xếp theo thứ tự. Nếu số lượng phần tử là lẻ, trung vị là phần tử ở vị trí ((n+1)/2), còn nếu là chẵn, trung vị là trung bình của hai phần tử giữa. Chính vì vậy, số trung vị thường được coi là một chỉ số thống kê ổn định hơn trong các tập dữ liệu có sự chênh lệch lớn giữa các giá trị.

Việc nắm rõ sự khác nhau giữa số trung bình và số trung vị giúp chúng ta lựa chọn phương pháp mô tả dữ liệu phù hợp hơn. Điều này rất quan trọng trong phân tích số liệu, đặc biệt khi chúng ta muốn tránh được những sai lệch trong các kết quả thống kê.

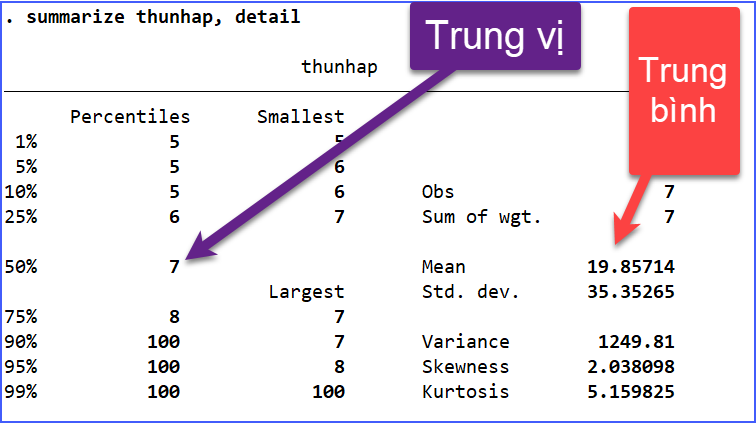
Khi nói về thống kê, trung bình và trung vị đều mang đến những góc nhìn thú vị về dữ liệu mà chúng ta đang trải nghiệm trong cuộc sống hàng ngày. Trong khi trung bình cho chúng ta cái nhìn tổng quan về một tập hợp các giá trị, thì trung vị lại giúp chúng ta hiểu rõ hơn về sự phân bố và những điểm đặc trưng trong dữ liệu. Việc nắm rõ hai khái niệm này sẽ giúp bạn phân tích thông tin một cách sâu sắc hơn, từ đó đưa ra những quyết định thông minh và hợp lý. Hãy áp dụng chúng vào cuộc sống và công việc, vì đôi khi, những điều ở giữa mới chính là chìa khóa giúp ta tìm ra hướng đi đúng đắn nhất.