Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Trong lĩnh vực công nghiệp và xây dựng, nhôm đang thớc bắc 3 là vật liệu được sử dụng rộng rãi nhờ những ưu điểm vượt trội về độ bền và tính ứng dụng đa dạng. Tuy nhiên, không phải ai cũng hiểu rõ về loại nhôm này cũng như sự khác biệt giữa nhôm đang thớc bắc 3 và các loại nhôm khác như đang bắc 1. Bài viết dưới đây sẽ giúp bạn tìm hiểu chi tiết về nhôm đang thớc bắc 3, từ quy trình sản xuất, tiêu chí đánh giá, hướng dẫn lựa chọn, đến bảng giá và lưu ý khi mua hàng, nhằm hỗ trợ bạn đưa ra quyết định chính xác nhất.
Hang Dang Thuc Bac 3
Hằng đẳng thức bậc 3 là một trong những khái niệm thú vị trong toán học, đặc biệt là ở cấp trung học cơ sở. Khi phân tích hằng đẳng thức này, chúng ta có thể thay thế các biểu thức A và B bằng những số cụ thể, từ đó dễ dàng nhận thấy tính đúng đắn của công thức. Ví dụ, với A^3 + B^3, chúng ta có thể sử dụng hằng đẳng thức (A + B)(A^2 – AB + B^2).
Không chỉ dừng lại ở đây, hằng đẳng thức bậc 3 còn bao gồm nhiều dạng khác nhau như lập phương của tổng và hiệu, hay hiệu hai lập phương. Điều này mang đến cho học sinh cơ hội khám phá và áp dụng vào các bài toán giải tích thực tiễn. Khi làm việc với những hằng đẳng thức này, các bạn có thể cảm nhận được sự giao thoa giữa lý thuyết và ứng dụng thực tế.
Chẳng hạn, với hằng đẳng thức A^3 – B^3 = (A – B)(A^2 + AB + B^2), ta dễ dàng nhận thấy rằng giá trị sẽ không thay đổi ngay cả khi các biến số được điều chỉnh. Tất cả những điều này tạo nên sự hấp dẫn trong quá trình học tập và nắm bắt kiến thức toán học.
Su Khac Biet Giua Hang Dang Thuc Bac 3 Va Hang Bac 1
Hằng đẳng thức bậc 2 và bậc 3 đều đóng vai trò quan trọng trong toán học, giúp chúng ta xử lý các biểu thức phức tạp một cách đơn giản hơn. Hằng đẳng thức bậc 2, như (a + b + c)², không chỉ giúp tính toán mà còn minh họa rõ nét cách tổng hợp các thành phần. Công thức này mở rộng qua nhiều khía cạnh, từ bình phương của tổng cho đến bình phương của hiệu, mang lại nhiều ứng dụng trong giải phương trình.
Trong khi đó, hằng đẳng thức bậc 3 lại là một bước tiến lớn hơn, như công thức lập phương của một tổng hay hiệu của hai lập phương. Điều này cho phép chúng ta khai thác những cấu trúc phức tạp hơn. Ví dụ, hiệu hai lập phương a³ − b³ có thể được biểu diễn dưới dạng (a − b)(a² + ab + b²), giúp việc giải các phương trình trở nên khả thi hơn.
Với bảy hằng đẳng thức đáng nhớ, học sinh lớp 8 được trang bị những công cụ mạnh mẽ để đối mặt với các hiện tượng đại số. Việc ghi nhớ những công thức này không chỉ là lý thuyết mà còn là hành trang hữu ích cho những ai muốn chinh phục toán học.
Quy Trinh San Xuat Hang Dang Thuc Bac 3
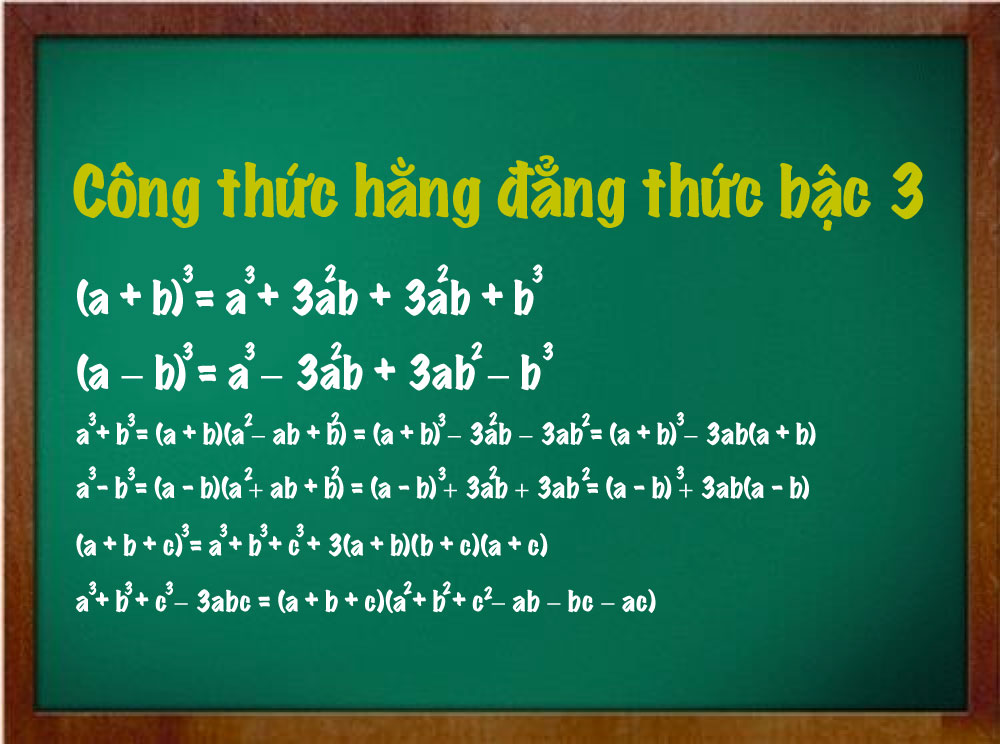
Hằng đẳng thức bậc 3 là một công cụ quan trọng trong đại số, giúp chúng ta xử lý các biểu thức đại số có dạng lập phương. Một trong những hằng đẳng thức nổi bật nhất là công thức \(A^3 – B^3 = (A – B)(A^2 + AB + B^2)\). Đây là cách tuyệt vời để phân tích đa thức thành nhân tử, giúp dễ dàng giải các phương trình.
Điều thú vị ở đây là \(A^2 + AB + B^2\) có thể coi như là bình phương thiếu của tổng \(A + B\). Nhờ vào điều này, chúng ta có thể đơn giản hóa những biểu thức phức tạp, làm cho việc giải phương trình trở nên dễ dàng hơn.
Hằng đẳng thức bậc 3 không chỉ có ý nghĩa lý thuyết. Trong thực tế, chúng ta có thể áp dụng hằng đẳng thức này để tính toán nhanh chóng và hiệu quả. Ví dụ, khi gặp phải vấn đề phân tích đa thức như \((x + 1)^3 + (x – 2)\), hằng đẳng thức này cho phép chúng ta tiếp cận bài toán một cách khoa học và có hệ thống.
Việc nắm vững hằng đẳng thức bậc 3 không chỉ nâng cao khả năng giao tiếp toán học mà còn là nền tảng vững chắc cho những kiến thức đại học sau này. Hãy tận dụng nó để trở thành những người giải toán giỏi nhé!
Tieu Chi Danh Gia Hang Dang Thuc Bac 3
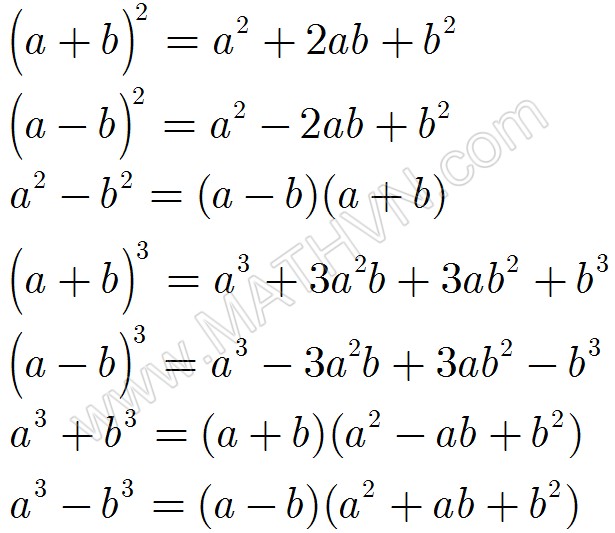
Hằng đẳng thức bậc 3 là một khái niệm quan trọng trong đại số, giúp chúng ta làm việc với các biểu thức bậc ba một cách hiệu quả. Dạng tổng quát của nó là ax³ + bx² + cx + d = 0, trong đó a, b, c, d là các hệ số và x là biến. Điều này không chỉ đơn thuần là một công thức, mà còn là một công cụ mạnh mẽ để giải quyết các phương trình phức tạp.
Một số hằng đẳng thức bậc 3 cơ bản thường được sử dụng bao gồm (a + b + c)³ = a³ + b³ + c³ + 3(a + b)(a + c)(b + c). Nhờ những công thức này, chúng ta có thể dễ dàng rút gọn và chuyển đổi các bài toán trở thành những dạng đơn giản hơn, thay vì phải trình bày từng bước chứng minh dài dòng.
Hơn nữa, các hằng đẳng thức như A³ – B³ = (A – B)(A² + AB + B²) giúp ta nhận thức rõ hơn về mối quan hệ giữa hai lập phương. Từ đó, chúng ta có thể áp dụng những kiến thức này vào các bài toán thực tế, giúp việc giải quyết trở nên nhanh chóng và hiệu quả hơn.
Hung Dan Lua Chon Hang Dang Thuc Bac 3
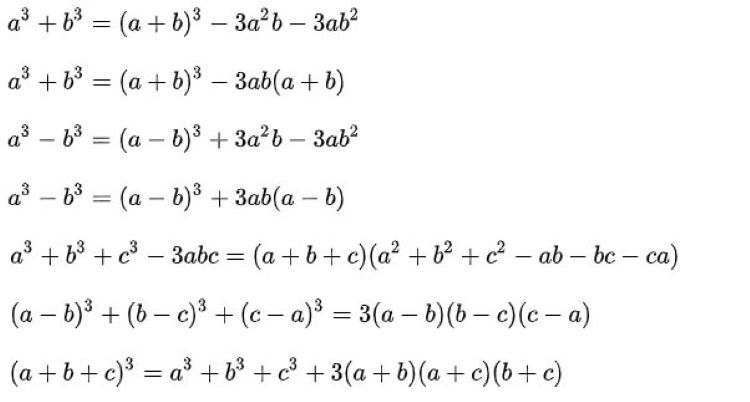
Hằng đẳng thức bậc 3 là một trong những khái niệm quan trọng trong toán học, giúp chúng ta đơn giản hóa và giải quyết các bài toán liên quan đến đa thức. Một công thức nổi bật mà chúng ta thường gặp là A³ – B³ = (A – B)(A² + AB + B²). Trong đó, A² + AB + B² có thể được coi là bình phương thiếu cho tổng A + B.
Việc áp dụng hằng đẳng thức này không chỉ giúp tiết kiệm thời gian trong quá trình giải toán mà còn tạo điều kiện thuận lợi cho việc phân tích đa thức bậc 3 thành nhân tử. Chắc hẳn bạn đã từng nghe đến các công thức khác như a³ + b³ = (a + b)(a² – ab + b²) hoặc a³ – b³ = (a – b)(a² + ab + b²). Những công thức này giúp việc giải các phương trình trở nên dễ dàng hơn.
Ngoài ra, việc ghi nhớ và phân tích các hằng đẳng thức cũng rất hữu ích trong các bài kiểm tra và kỳ thi. Hãy luyện tập nhiều với các ví dụ thực tế để nắm vững kiến thức, từ đó đạt được kết quả cao trong học tập cũng như trong các kỳ thi.
Bao Gia Hang Dang Thuc Bac 3
Hằng đẳng thức bậc 3 là một trong những công thức quan trọng trong toán học, giúp chúng ta giải quyết các biểu thức bậc ba một cách hiệu quả. Công thức cơ bản nhất có dạng \( ax^3 + bx^2 + cx + d = 0 \), trong đó \( a, b, c, d \) là các hệ số của đa thức. Điều thú vị là chúng ta có thể chia hằng đẳng thức bậc 3 thành nhiều dạng khác nhau như lập phương của một tổng, lập phương của một hiệu, hay hiệu của hai lập phương.
Một trong những công thức nổi bật của hằng đẳng thức bậc 3 là lập phương của một tổng: \( (A + B)^3 = A^3 + 3A^2B + 3AB^2 + B^3 \) và lập phương của một hiệu: \( (A – B)^3 = A^3 – 3A^2B + 3AB^2 – B^3 \). Những công thức này không chỉ đơn giản hóa việc tính toán mà còn giúp chúng ta nhận diện và áp dụng chúng trong các bài toán thực tế.
Ngoài ra, tổng của hai lập phương \( A^3 + B^3 \) có thể được viết dưới dạng \( (A + B)(A^2 – AB + B^2) \), điều này cho phép chúng ta nhanh chóng tìm ra kết quả mà không cần phải tính từng phần riêng lẻ. Những hằng đẳng thức này không chỉ có giá trị lý thuyết mà còn mang lại những ứng dụng thiết thực trong nhiều lĩnh vực toán học khác nhau.
Ung Dung Cua Hang Dang Thuc Bac 3
Hằng đẳng thức bậc 3 có vai trò hết sức quan trọng trong việc giải quyết các bài toán toán học, đặc biệt là trong kỳ tuyển sinh vào lớp 10 chuyên toán của Bình Định những năm 2025 và 2026. Những công thức hằng đẳng thức này giúp học sinh không chỉ nắm vững lý thuyết mà còn có thể áp dụng vào thực tiễn.
Một trong những ứng dụng thiết thực của hằng đẳng thức bậc 3 là trong việc giải phương trình bậc 3. Nhờ vào công thức Viète và các công thức đáng nhớ như lập phương của một tổng hoặc hiệu, học sinh có thể tính toán nhanh chóng hơn, từ đó giải quyết được các bài toán phức tạp hơn.
Ngoài ra, việc vận dụng hằng đẳng thức còn giúp học sinh phát triển kỹ năng tư duy logic, từ việc tính toán cho đến thiết kế mô hình toán học. Khi làm quen với các công thức mở rộng của hằng đẳng thức, học sinh không chỉ học để thi mà còn có thể áp dụng vào việc giải các bài toán thực tế trong cuộc sống hàng ngày. Thật vậy, hằng đẳng thức bậc 3 mở ra cánh cửa mới cho sự hiểu biết và sáng tạo trong toán học!
Mua Hang Dang Thuc Bac 3 O Dau
Hằng đẳng thức bậc 3 là một khái niệm thú vị trong toán học, thường được sử dụng để mở rộng và giải quyết các biểu thức bậc ba. Định nghĩa cơ bản của nó là một phương trình có dạng ax^3 + bx^2 + cx + d = 0, trong đó a, b, c, d là các hệ số và x là biến. Hằng đẳng thức này không chỉ giúp rút gọn các phép toán phức tạp mà còn mang lại cái nhìn sâu hơn về mối quan hệ giữa các đại lượng.
Có hai công thức hằng đẳng thức bậc 3 rất quan trọng mà bạn có thể dễ dàng nhớ và áp dụng. Đầu tiên là (A + B)³ = A³ + 3A²B + 3AB² + B³, và thứ hai là (A – B)³ = A³ – 3A²B + 3AB² – B³. Những công thức này không chỉ hữu ích trong việc tính toán mà còn như những “đường tắt” giúp bạn xử lý nhanh chóng các bài toán phức tạp trong chương trình toán học.
Ngoài ra, các hằng đẳng thức mở rộng như (a + b + c)³ = a³ + b³ + c³ + 3(a + b)(a + c)(b + c) cũng là những kiến thức đáng nhớ. Nắm vững chúng không chỉ giúp các bạn tự tin hơn trong các bài kiểm tra mà còn phục vụ tốt trong các tình huống thực tiễn khi giải quyết các vấn đề liên quan đến đại số.
Luu Y Khi Mua Hang Dang Thuc Bac 3
Khi mua hàng liên quan đến hằng đẳng thức bậc 3, bạn cần chú ý đến những công thức cơ bản nhưng quan trọng. Hằng đẳng thức này không chỉ đơn thuần là lý thuyết mà còn có ứng dụng thực tiễn trong các bài toán. Một trong những công thức phổ biến là A³ – B³ = (A – B)(A² + AB + B²), với điều kiện A và B là các biểu thức tùy ý.
Để dễ dàng áp dụng hằng đẳng thức, hãy chú ý đến sự đối xứng giữa các số hạng. Điều này sẽ giúp bạn nhận diện được các phần quan trọng trong bài toán một cách nhanh chóng. Bạn cũng nên nhớ rằng hằng đẳng thức bậc 3 thường xuất hiện trong các bài tập lớp 8, họ sẽ giúp bạn củng cố kiến thức và kỹ năng giải toán.
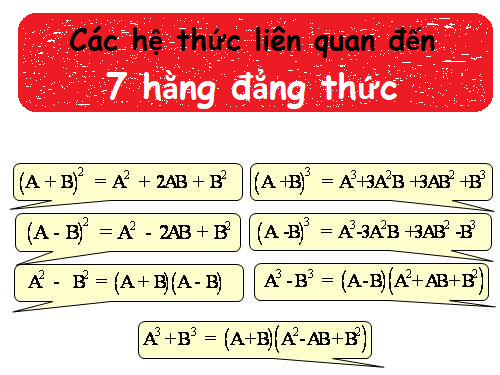
Ngoài ra, khi áp dụng bất đẳng thức AM-GM cho các số thực dương, bạn cũng nên chú ý đến các điều kiện đã cho. Việc nắm vững lý thuyết cùng với phương pháp giải sẽ giúp bạn tự tin hơn khi làm bài. Hãy ghi nhớ 7 hằng đẳng thức đáng nhớ, chúng sẽ trở thành “cẩm nang” không thể thiếu trong quá trình học tập.
Kết thúc bài viết về Hang Dang Thuc Bac, có thể nhấn mạnh rằng nơi đây không chỉ đơn thuần là một điểm du lịch, mà còn là biểu tượng của sự hòa quyện giữa thiên nhiên và văn hóa. Những giá trị lịch sử, truyền thống và sự phong phú của hệ sinh thái tại hang chắc chắn sẽ để lại ấn tượng sâu sắc trong lòng mỗi du khách. Việc bảo tồn và phát huy giá trị của Hang Dang Thuc Bac không chỉ mang lại lợi ích cho du lịch địa phương, mà còn góp phần gìn giữ di sản văn hóa thiên nhiên cho các thế hệ mai sau. Hãy cùng chung tay bảo vệ và tôn vinh những nét đẹp quý giá này!
